la configuración de X que corresponde a un valor o rango de valores deseados para Ts, prediciendo su valor.

RESULTADOS. Ecuación para el elemento dos: 𝑇𝑠 = 1,240 + 0,03785𝑋 y del elemento cinco: 𝑇𝑠 = 0,4354 + 0,011418 𝑋, que sustituyendo el valor de X para la estandarización de la operación de llenado de recipientes con líquidos ubicándolos en paquetes con una capacidad de 24, la producción diaria estandarizada es de 22 paquetes por día, procesándose 528 recipientes.

Palabras clave: datos estándar, Minitab, operación, regresión lineal simple.

ABSTRACT

Minitab software in standard weather prediction. INTRODUCTION. The study includes a bibliographic review, linear regression concepts, applications, the characterization of standard data methods and Minitab 20 software. OBJECTIVE. Calculate the standard time of the variable elements of an operation through data tables in excell, processing them in Minitab 20 with greater precision and speed, until the standard time of the operation is determined. METHOD. A statistically significant relationship does not imply that X is the cause of Y, the equations adjusted for the linear model with the processing of data recorded in files processed in the statistical software allow to find the configuration of X that corresponds to a desired value or range of values for Ts, predicting its value. RESULTS. Equation for element two:Ts = 1.240 + 0.03785X and of element five:Ts = 0.4354 +0.011418 X, which substituting the value of X for the standardization of the operation of filling containers with liquids placing them in packages with a capacity of 24, the standardized daily production is 22 packages per day, processing 528 containers.

Key words: standard data, Minitab, operation, simple linear regression.

INTRODUCCIÓN

Minitab 2020, ofrece la posibilidad de realizar una regresión lineal simple a través de su Asistente que incluye, los procedimientos "Paso a Paso" y "Mejor Subconjunto". La estadística es fundamental a la hora de tomar decisiones a partir de patrones de comportamiento basados en el análisis y recolección de datos, estudio, posterior procesamiento y clasificación. Hoy, gracias al Big Data, se trata de una disciplina que ha cobrado todavía mayor fuerza e interés, por lo que es fundamental disponer de un buen software que sea capaz de ayudarnos a entender y simplificar la complejidad de los grandes volúmenes de datos [1].

Entre la enorme variedad de sus aplicaciones, resulta importante mencionar la propuesta por el economista estadounidense de origen ruso Wassily Leontief (1905-

1999), quien en 1073 fue galardonado con el premio Nobel de Economía por “El desarrollo del método input-output y su aplicación en los problemas económicos de mayor importancia”. Su análisis supuso la introducción del algebra matricial al tratamiento de los problemas del equilibrio general, con lo que se desarrolló un modelo estático muy operativo para estimar los niveles productivos sectoriales y las relaciones intersectoriales [2]

La regresión lineal simple es útil para encontrar la fuerza o magnitud de cómo se relacionan dos variables: una independiente, que se representa con una X, y otra dependiente, que se identifica con una Y; sin embargo, la regresión lineal simple se distingue de otras pruebas, pues con ella puede estimarse o predecirse el valor de la variable de respuesta a partir de un valor dado a la variable explicativa. Para asociar estas dos variables se propone una línea recta –que describe la tendencia de los datos, de ahí el nombre de regresión lineal. Dicha recta se expone en un plano y su grado de inclinación representa la pendiente, y una inclinación muy destacada indica grandes cambios en la variable dependiente [3]

Las ecuaciones lineales, así como colecciones de las mismas, denominadas sistemas

(de ecuaciones lineales) surgen tanto en problemas de naturaleza práctica como teórica.

En la ciencia la industria, el comercio, entre otras actividades y ramas del quehacer humano, es común el modelar problemas reales por medio de sistemas lineales; de allí la importancia de disponer de técnicas de análisis y solución, si existen, de los mismos [3]. En la presente investigación relacionamos estas conceptualizaciones en los elementos variables de las operaciones de un proceso con el objetivo de estandarizar sus tiempos sin aplicar técnicas de la medición del trabajo.

La medición del trabajo es la aplicación de técnicas para determinar el tiempo que invierte un trabajador, en condiciones normales, en realizar una tarea definida, efectuándola según el método normalizado de ejecución. Históricamente, el estudio de tiempo, tal y como fue creado por Taylor, se empleaba para establecer las normas de tiempo para el rendimiento del trabajo. En tanto, el estudio de los movimientos, tal como fue creado por el matrimonio Gilbreth, estaba dirigido a mejorar la forma en que se llevaba a cabo el trabajo. A través de los años, las dos disciplinas se entrelazaron, para apoyarse y complementarse entre sí. En la actualidad, el trabajo se mide por medio de dos métodos: el cronometraje continuo y el cronometraje con vuelta a cero [4], ¿Y qué sucede cuando ya tenemos los procesos estandarizados?, la respuesta a esta interrogante será dada en esta investigación que está con el cálculo más utilizado en datos estándar y es el método de modelo de regresión lineal utilizando el Software Minitab 2020.

El objeto investigado es la operación de: llenado de recipientes con líquidos ubicándolos en paquetes, los mismos tienen una capacidad de (2, 3, 4, 6 y 12) recipientes, encontrándose estandarizados, analizar la producción estándar por día del mismo producto pero con una nueva presentación de un paquete con 24 recipientes, es lo que nos llevó a investigar, valorando aumentar las ventas y mantener los niveles de utilidades, pudimos hacerlo con el uso del Software estadístico Minitab, con modelos simples, obteniendo de forma oportuna las estandarizaciones de los elementos variables, utilizando la información digital archivada de los tiempos estandarizados de los elementos que aplican, luego se procedido a totalizar los tiempos de los elementos para obtener el tiempo total estándar y la producción estándar por día.

MATERIALES Y MÉTODOS

Muestra: Esta operación cuenta con los valores de X que se establecen con anticipación que son las presentaciones de los paquetes con la cantidad de: 2, 3, 4, 6 y 12 recipientes, n= 5, se recolecta de forma aleatoria de elementos que son representativos de la operación en estudio. Los datos de Y no necesitan estar distribuidos normalmente y serán referidos como los tiempos estándar (Ts), que ya han sido obtenidos de los archivos digitales donde la ecuación no será utilizada más allá del rango de los valores de X de su muestra, que en esta investigación solo será aplicada para determinar los datos estándar de los elementos variables dos y cinco con un paquete de una nueva presentación con capacidad para 22 recipientes .Está operación ya se encuentra estandarizada para analizar la producción estándar por día del mismo producto pero con una presentación diferente, valorando aumentar las ventas y mantener los niveles de utilidades, se emplea el Software estadístico Minitab, con modelos simples, obteniendo de forma oportuna las estandarizaciones de dos elementos, solo se necesita la información digital archivada de los tiempos estandarizados de los elementos y se utilizan los que apliquen, luego totaliza los tiempos de los elementos para obtener el tiempo total, ya sea normal o estándar

Normas éticas de investigación

El enfoque de esta investigación está basado en una metodología cuantitativa, debido a que se utilizan datos numéricos para la aplicación de regresión lineal simple en los elementos variables de una operación, y posteriormente calcular el tiempo estándar de la operación igualándose al tiempo de ciclo de la misma, que nos lleva a poder determinar la cantidad de recipientes que pueden ser procesados en una jornada prevista para cuatrocientos ochenta minutos.

Instrumentos y herramientas: Se determina la ecuación de la recta donde (y) se sustituye por 𝑇𝑠, quedando 𝑇𝑠 = 𝑎 + 𝑏𝑥, x y 𝑇𝑠 son coordenadas de un punto, b es la pendiente y a es la coordenada y de la intersección en 𝑇𝑠. Ya que esta ecuación describe una recta en términos de su pendiente y su intersección en 𝑇𝑠, se dice que esta ecuación está en su forma pendiente- intersección. Cuando trabajamos con estas relaciones lineales, la forma pendiente- intersección nos ayuda a traducir entre la gráfica de una recta y la ecuación de una recta, con el uso del Software Minitab 20 y el Excel.

Técnicas de análisis de datos: Pruebas de significación para la regresión lineal, la ecuación de regresión lineal simple indica que el valor medio o valor esperado de 𝑇𝑠 es una función lineal de x: E (𝑇𝑠/x) = a + b x. Si b=0 entonces E (𝑇𝑠 /x) = a y en este caso el valor medio no depende del valor de x, y concluimos que x y 𝑇𝑠 no tienen relación lineal. En forma alternativa, si el valor b= 0 llegamos a la conclusión que las dos variables se relacionan (más específicamente, que hay una componente lineal en el modelo). Existen dos pruebas, por lo menos, que se pueden utilizar para tal fin.

Procedimiento: Se pueden definir los datos estándar a la recopilación de datos de una variedad de elementos por medio de estudios de tiempos con cronómetro para luego desarrollar normas de tiempos para otras tareas. Para poder desarrollar un tiempo normal o estándar para un nuevo trabajo utilizando datos estándar, se realiza lo siguiente:

1. Analizar el nuevo trabajo y dividirlo en elementos.

2. Buscar en los archivos los tiempos de los elementos y utilizar los que se apliquen.

3. Totalizar los tiempos de los elementos para obtener el tiempo total, ya sea normal o estándar. Con este sistema no es necesario medir directamente la operación o el trabajo que se va a desarrollar, ni tampoco es necesario observar la operación para establecer los tiempos normales o estándar; ya que únicamente se necesitarán los archivos de trabajos relacionados al mismo. Por lo general este método expresa la relación que existe entre algunas características de un trabajo y el tiempo que se requiere para su ejecución. Estos tiempos son relativamente congruentes, ya que los elementos tabulados comprendidos por: Los datos obtenidos deberán ser archivados por medio de un índice y se puede considerar de la siguiente manera: constantes y variables

Un elemento constante es aquél en el que el tiempo asignado permanecerá aproximadamente el mismo para cualquier pieza y un elemento variable es aquél en el que el tiempo asignado no será el mismo dentro de una variedad específica de trabajos.

El procedimiento para obtener los datos estándar por Lo general se asemeja al requerido para desarrollar cualquier procedimiento de predicción, por lo que es siempre indispensable realizar los siguientes seis pasos:

1. Obtener los estándares de tiempo que cubran un nivel amplio dentro de un grupo de trabajos similares.

2. Resumir los datos en una hoja.

3. Ver cuáles son los elementos variables y cuáles los constantes.

4. En los elementos constantes determinar el tiempo promedio.

5. En los elementos variables determinar los factores causales y su relación con el tiempo estándar.

6. Preparar los datos estándar elementales para el desarrollo de tiempos estándar para tareas Nuevas.

Luego en esta investigación después de aplicar este método a través de tablas de Excel, es que se procede a procesar toda la información en el Minitab 20, donde se realiza con mayor precisión y menor tiempo.

RESULTADOS

Caracterización de la operación: Llenado de recipientes con líquidos ubicándolos en paquetes. La jornada laboral está prevista para ocho horas al día, se toman cuatrocientos ochenta minutos, como no es objeto de esa investigación no se van a restar los suplementos y tolerancias, los elementos de la operación son: 1. Colocar recipiente en el paquete, 2. llevar paquetes a la llenadora, 3. Llenar un recipiente y colocarle tapa, 4. Colocar recipientes llenos en los paquetes y 5. Llevar paquetes al almacén.

En la tabla 1, se muestran las presentaciones actuales de los recipientes con líquidos que son sacados con diferentes capacidades.

Tabla 1. Presentaciones actuales de los paquetes con el número de recipientes

TIPO DE PAQUETE	NÚMERO DE RECIPIENTES POR PAQUETES
A	2
B	3
C	4
D	6
E	12

En los archivos encontramos los siguientes datos:

Tabla 2. Tiempo estándar en minutos por recipiente, procesado en cada uno de los elementos de la operación

ELEMENTOS DE LA OPERACIÓN	TIEMPO ESTÁNDAR EN MINUTOS POR RECIPIENTE
1. Colocar recipiente en el paquete	0,04
3.Llenar un recipiente y colocarle tapa	0,25
4.Colocar recipientes llenos en los paquetes	0,19

Tabla 3. Tiempo estándar en minutos de los elementos dos y cinco, en las diferentes presentaciones ya estandarizadas

TIEMPO ESTÁNDAR EN MINUTOS

DEL ELEMENTO

TIPO DE PAQUETE	DOS	CINCO
A	1,20	0,45
B	1,34	0,48
C	1,48	0,50
D	1,56	0,53
E	1,64	0,60

Perspectiva metodológica

Cuando se refiere a la predicción es a un método de cálculo más utilizado en datos estándar y en este caso el método de regresión o mínimos cuadrados.

Para modelar la relación entre una variable X y una variable de respuesta 𝑇𝑠, se utiliza la regresión simple con las siguientes formulas:

𝑇_𝑠 = 𝑎 + 𝑏_𝑥

(1)

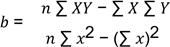(2)

𝑎 =

(∑ 𝑦 ∑ 𝑥²) − (∑ 𝑥 ∑ 𝑥𝑦)

𝑛 ∑ 𝑥²− (∑ 𝑥)²

(3)

Recolección de datos

Los valores de X los vamos a establecer con anticipación, de lo contrario pueden ser incluidos en la muestra de elementos con cualquier valor de X

La muestra se recolectará de forma aleatoria de elementos que sean representativos de la operación en estudio

La muestra recolectada es suficientemente grande

Los datos serán registrados en el orden de recolección

Los datos de Y no necesitan estar distribuidos normalmente

La ecuación no será utilizada más allá del rango de los valores de X de su muestra

Los procesos ya se encuentran estandarizados y se analiza la producción estándar por día del mismo producto pero con presentaciones diferentes, valorando aumentar las ventas y mantener los niveles de utilidades, podemos hacerlo con el uso del Software estadístico, con modelos simples, obteniendo de forma oportuna las estandarizaciones de las operaciones, solo necesitándose la información digital archivada de los tiempos estandarizados de los elementos y utilizar los que se apliquen, luego totalizar los tiempos de los elementos para obtener el tiempo total, ya sea normal o estándar.

Partiendo que se realiza el procedimiento descrito anteriormente se calcula posterior el tiempo estándar, se toman los datos archivados, se consolida y la operación en estudio queda con los datos de la tabla 4.

Tabla 4. Estandarización obtenida de los estándares por elementos y capacidad de los paquetes

CAPACIDAD DE LOS PAQUETES	2	3 4 6 12				24
ELEMENTO		TIEMPO ESTÁNDAR EN MINUTOS
	A	B	C	D	E	F
1. Colocar recipiente en el paquete	0,08	0,12	0,16	0,24	0,48	0,96
2. Llevar paquetes a la llenadora	1,20	1,34	1,48	1,56	1,64	?
3.Llenar un recipiente y colocarle tapa	0,50	0,75	1,00	1,50	3,00	6,00
4. Colocar recipientes llenos en los paquetes	0,38	0,57	0,76	1,14	2,28	4,56
5. Llevar paquetes al almacén.	0,45	0,48	0,50	0,53	0,60	?
TOTAL, DEL TIEMPO ESTÁNDAR	2,61	3,26	3,90	4,97	8,00	?

Cálculo del tiempo estándar del elemento número dos

Primeramente, se procesa toda la información, hasta obtener el resultado del tiempo estándar en minutos, con el Excel se obtuvo:

Tabla 5. Datos primarios para el cálculo del tiempo estándar del elemento número 2; Llevar paquetes a la llenadora.

1,48 4 16 5,92

1,56 6 36 9,36

1,64 12 144 19,68

∑ 𝑇_𝑠 = 7,22 ∑ 𝑥 = 27 ∑ 𝑥² = 209 ∑(𝑥)(𝑇_𝑠) = 41,38

(∑ 𝑥)² =729

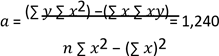
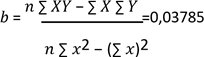
𝑇_𝑠 = 𝑎 + 𝑏_𝑥

𝑇_𝑠 = 1,240 + (0,03785)(24 𝑟𝑒𝑐𝑖𝑝𝑖𝑒𝑛𝑡𝑒𝑠)

𝑇_𝑠 = 2,1480 minutos para llevar paquetes de 24 recipientes a la llenadora.

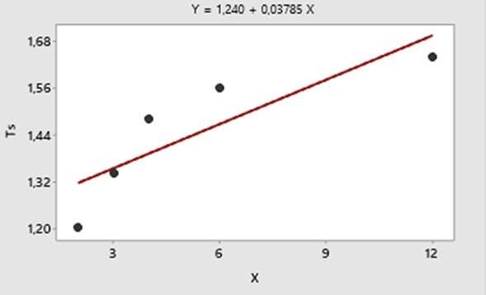
Se procesa toda la información en el Minitab 20, como se muestra en la Gráfica 1.

Gráfica 1. Línea ajustada para modelo lineal

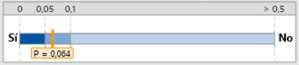
En la Gráfica 2, se puede dar respuesta a la interrogante ¿Existe una relación entre Ts y X?, siendo que no es estadísticamente significativa (p >0,05)

Gráfica 2. Relación entre Ts y X

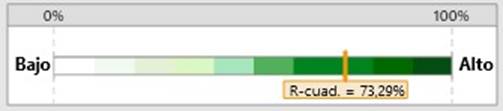
El modelo de regresión puede explicar 73,29 % de la variación en Ts.

Gráfica 3. Porciento de variación explicado por el modelo.

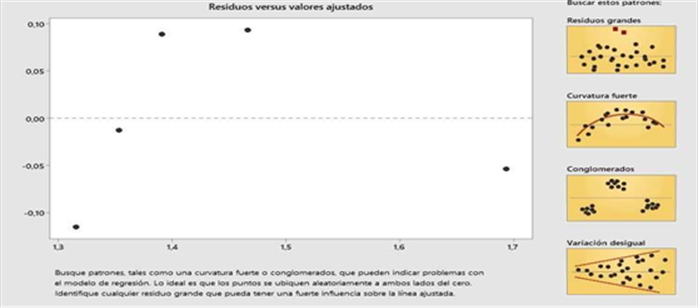
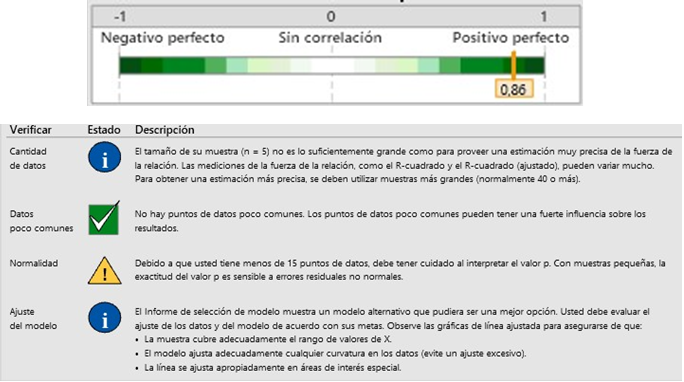
La correlación entre Ts y X, no es estadísticamente significativa (p>0,05)

Gráfica 4. Correlación entre Ts y X. Tarjeta de informe

Cálculo del tiempo estándar del elemento número cinco

Se toman los tiempos estándar del elemento: Llevar paquetes al almacén, en las diferentes presentaciones que se fabrican actualmente, es decir, con capacidades para:2,3,4,6 y 12 recipientes, para proceder con la determinación de a y b, y poder a través de la regresión lineal determinar cuál es el tiempo de este elemento, Tabla 6.

Tabla 6. Datos primarios para el cálculo del tiempo estándar del elemento número 5; Llevar paquetes al almacén.

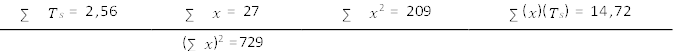
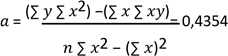
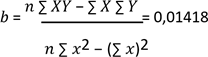
𝑇_𝑠 = 𝑎 + 𝑏_𝑥

𝑇_𝑠 = 0,4354 + (0,01418) (24 𝑟𝑒𝑐𝑖𝑝𝑖𝑒𝑛𝑡𝑒𝑠)

𝑇_𝑠 = 0,7757 minutos para Llevar paquetes de 24 recipientes al almacén.

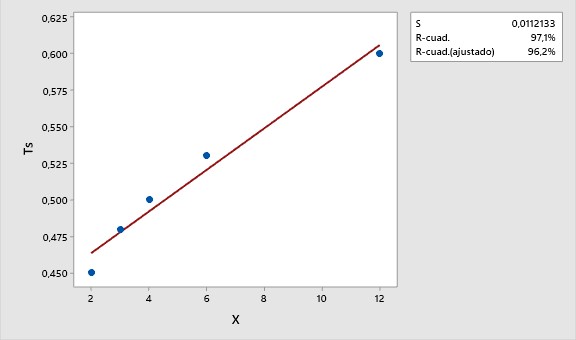
El modelo de regresión lineal, se comprueba en el software Minitab 20, como se muestra en la Gráfica 5.

Resumen del modelo

R-cuad.

S R-cuad. (ajustado)

0,0112133 97,12% 96,15%

Análisis de Varianza

Fuente GL SC MC

Regresión 1 0,0127028 0,0127028 101,03 0,002

Error 3 0,0003772 0,0001257

Total 4 0,0130800

Gráfica 5. Gráfica de línea ajustada, Ts = 0,4354 + 0,01418 x

Gráfica 6. Relación entre Ts y X

Gráfica 7. Regresión para Ts vs.X, Tarjeta de informe

Para conocer el tiempo estándar de toda la operación LLENADO DE LÍQUIDOS EN RECIPIENTES UBICANDOLOS EN PAQUETES, del paquete con una capacidad de 24 recipientes, únicamente se deben sumar los valores de todos los elementos, Tabla 7.

Tabla 7. Tiempo estándar de la operación en estudio.

ELEMENTO	TIEMPO EN MINUTOS
1. Colocar recipiente en el paquete	0,96
2.llevar paquetes a la llenadora	2,15
3.Llenar un recipiente y colocarle tapa	13,20
4.Colocar recipientes llenos en los paquetes	4,56
5.Llevar paquetes al almacén.	0,78
TIEMPO ESTÁNDAR	21,64

DISCUSIÓN Y CONCLUSIONES

El modelo lineal de la ecuación ajustada que describe la relación entre Ts y X del elemento dos: Ts= 1,240 + 0,03785 X, Si el modelo se ajusta adecuadamente a los datos, esta ecuación se puede utilizar para predecir Ts para un valor de X, o hallar la configuración de X que corresponde a un valor o rango de valores deseados para Ts que para llevar un paquete de 24 recipientes a la llenadora se obtiene un valor de 2,15 minutos. Una relación estadísticamente significativa no implica que X sea la causa de Ts.

La ecuación ajustada: Ts =0,4354 + 0,01418 X, describe una relación entre Ts y X, si el modelo se ajusta adecuadamente a los datos se puede predecir Ts, si X toma un valor de 24 se obtiene 0,78 minutos llevar paquetes al almacén. El modelo de regresión puede explicar 97,12 % de la variación en Ts, con una correlación positiva (r=0,99) que indica que cuando X aumenta Ts también tiende a aumentar, siendo la relación entre las dos variables estadísticamente significativa (p<0,05)

Con el Software Minitab 20, modelos de regresión y gráficas de línea ajustada se puede calcular los valores de datos estándar en los elementos variables, que sumándole los obtenidos de los elementos constantes a través de la búsqueda en los archivos, se puede totalizar hasta obtener el tiempo de ciclo estandarizado de cualquier operación, en esta investigación se obtuvo un resultado de 22 paquetes por día con una capacidad de 24 recipientes.

REFERENCIAS

A. A, Probability, Statistics, and Queueing Theory, New York: Academic Press, 2014.

E. G. G. -. S. I. O. García, Álgebra lineal y sus aplicaciones, Grupo Editorial Patria, 2016.

A. &. Z. M. M. &. L. A. J. Reding Bernal, «¿Cómo y cuándo realizar un análisis de regresión lineal simple? Aplicación e interpretación,» Dermatología Revista Mexicana, vol. 55, nº 6, pp. 395-402, 211.

Manual de álgebra lineal, Colombia: Universidad del Norte, 2017.

J. L. P. E. A. J. M. A. R. Pérez, Estudio del trabajo: una nueva visión., México D.F: Grupo Editorial Patria, 2015.

R. B. Chase, R. F. Jacobs y N. J. Aquilano, Administración de operaciones producción y cadena de suministros, México D.F.: McGraw-Hill, 2009.

R. Z.-C. V. R.-S. Marco Antonio Díaz-Martínez, «Simulación con Flexsim, una nueva alternativa,» Cientifica, vol. 22, nº 2, pp. 97-104, 2018.

F. s. Hillier y G. J. Lieberman, Introducción a la investigación de operaciones, México D.F.: McGraw-Hill, 2010, p. 778.

R. S. Kaplan y D. P. Norton, Cuadro de Mando Integral, Barcelona: Gestión 2000, 2002.

W. WL, Investigación de Operaciones. Aplicaciones y Algoritmos. 4ta ed, Stamford: Thomson Internacional, 2015.

T. J. G. D. H. C. Shortle JF, Fundamentals of Queueing Theory, New York, 2017.

A. S, Applied Probability and Queues, New York: Springer–Verlag, 2013.

M. D. Haghighi AM, Delayed and Network Queues, New York: John Wiley & Sons, 2016.

A. G. G. E. L. y. W. M. Beaverstock, Applied Simulation Modeling and Analysis using FlexSim.FlexSim Software Products, 2015: Orem USA.

&. D. G. O. K. D. Tocher, The Automatic Programming of Simulations, Proceedings of the Second International Conference on Operational Research, pp 50 - 68, 1960.

L. A. M. &. A. Inc, Simulation Modeling and Analysis, 4a ed., Tucson, Arizona, U.S.A: McGraw - Hill, 2007, pp. 1-273.